(Confounding the 2k Factorial Design in Four Blocks)
建构一个交络于4个集区而每个集区有2k-2个观测值的2k因子设计是有可能的,这种设计对于因子个数k>= 4而集区大小却相当小时特别有效。
兹考虑25设计,如每个集区只能容纳8次试验,则需要4个集区,选出2个效果交络于集区,如ADE与BCE,此二个效果所对应之定义对比为,
L1 = x1+ x4 + x5
L2 = x2+ x3 + x5
则每一个处理组合会产生一个L1 (Mod 2)与L2 (Mod 2)的特定成对值,即(L1 , L2)= (0, 0), (0, 1), (1, 0),或(1, 1),产生相同的(L1 , L2)值的处理组合将被指订至同一集区,如,
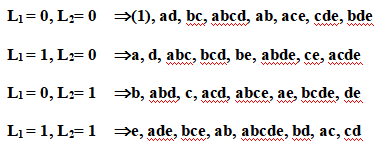
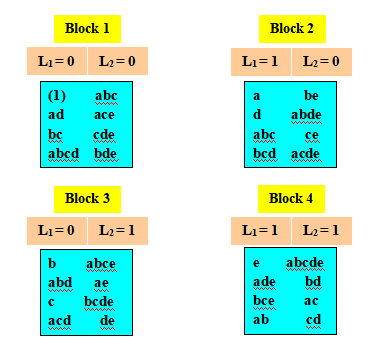
图7-5 交络ADE, BCE与ABCD之4个集区之25设计
仔细思量,除了ADE与BCE外,尚有另一个效果被集区交络,因4个集区有3个自由度,而ADE与BCE各有1个自由度,明显地另有一个1个自由度的效果亦被交络矣,此即ADE与BCE的广义交互作用(Generalized Interaction),其定义为ADE与BCE的乘积Mod 2,因此,ADE与BCE的广义交互作用为(ADE)(BCE) = ABCDE2 = ABCD ,且亦交络于集区。
注意,对某个特定集区里的任何2个效果的符号相乘(e.g., ADE与BCE)带来该集区另一个效果的符号(即ABCD)。因此,ADE,BCE与ABCD都是交络于集区。
由25设计的正负符号,可知处理组合被指派至集区如下
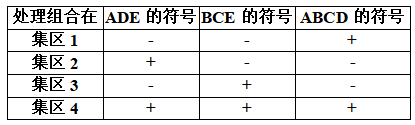
在上节7-4中提及之主集区的群理论性质仍成立,主集区里的2个处理组合的乘积产生主集区里的另一个元素,亦即,如,
ad × bc = abcd; abe × bde = ab2de2 = ad
要建构另一集区,则选一个不在主集区里之处理组合(如b)与主集区里的处理组合乘以b,则,
b × (1) = b; b × ad = abd;
b × bc = c; b × abcd = acd
如此会产生集区3里之8个处理组合。实务上,主集区可以从定义对比与群理论性质得到,而其他集区之处理组合由
述方法决定。建构一个4集区的2k设计的一般步骤:
◎ 选择2效果与集区交络,自然会有第3个效果(即是前2个的广义交互作用)与集区交络,
◎ 利用2个定义对比(L1 , L2)与主集区的群理论性质来建构所要的设计,
◎ 在选择交络于集区之效果时务必谨慎,以免有兴趣的效果被交络。
牺牲3因子交互作用的信息比牺牲2因子交互作用更合意
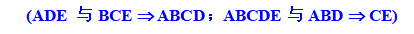
2021/1/14 16:29:57
2021/1/27 17:05:39
2021/3/10 15:48:49
2021/4/8 14:42:32
2021/1/8 16:32:33

我们不单提供专业的软件与服务,我们同时也为客户系统的运行提供理论与经验支持,分享我们在质量管理领域的相关经验与知识!