当因子数目很小时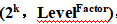，如k = 2或3，通常有必要反覆实验以获得一个误差估计值。如23因子实验必须以2个集区来进行且ABC被交络，实验者决定反覆设计4次，如下图，

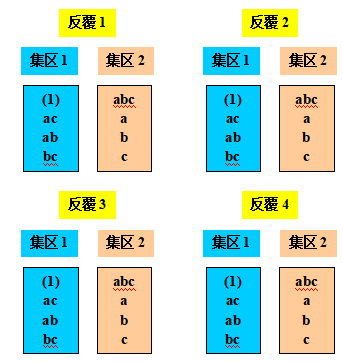
此设计总共32个观测值和31个自由度，有8个集区即7个自由度，此7个自由度分解为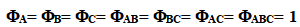，而误差平方为反覆与因子效果(A, B, C, AB, AC, BC)之二者交互作用。

考虑视交互作用为零且将其均方作为误差估计值的作法是成立的，此均方误差可以检定主效果与2-因子交互作用效果。

倘实验资源允许反覆的交络设计，较佳方式是稍微以不同方式来设计各个反覆的集区，此方式包括在每个反覆中交络不同的效果，使得所有的效果都能有一些信息，此法称之为部分交络(Partial Confounding)。倘k 不算太小，即k ³ 4，且只一次反覆时，实验者常假设高阶交互作用效果是可忽略的，并将其平和合并为误差。

范例7-2

回顾再续范例6-2，一个化学产品于一压力槽内生产，在实验工厂进行因子实验来研究产品的过滤比率(Filtration Rate)，4个因子为温度(A)、压力(B)、甲醛浓度(C)、与搅拌速度(D)，各因子均有2水平，单次反覆。有兴趣于极大化过滤比率。

用此实验来说明一个未反覆设计集区划分与交络的概念，假设2⁴ = 16种处理组合无法利用一批原料进行所有的试验，实验者由一批原料可以试验8个处理组合，所以一个2⁴ 交络于2个集区的设计是适当的，且交络最高阶交互作用效果(ABCD)于集区。

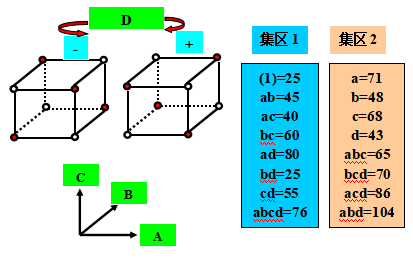
假设二批原料中有一批的质量低劣，造成所有的反应值均比用另一批原料所得值低20，即原始反应值减去20，低劣质量原料是集区1与良好质量原料批为集区2。计算结果，

◎ 4个主效果、6个2-因子交互作用效果、4个3-因子交互作用效果的估计值均与无集区效果的例6-2所得之效果估计值完全相同。当划出这些效果估计值的常态机率图时，因子A、C、D与AC、AD交互作用为显著重要效果。

◎ ABCD交互作用效果的估计值原为1.375，但在此实验其估计值为-18.625，因ABCD交络于集区，ABCD交互作用效果的估计值是原1.375加上区集效果(-20)，即ABCD = 1.375+(-20)= -18.625。集区效果亦可由二个集区平均反应差得之，即

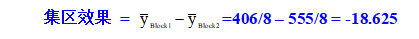
所以，此效果真正估计= 集区 + ABCD

◎ 此实验倘非以集区方式进行，且前8次试验均减去20，则结果可能会非常不同。