根据过程质量的客观分布规律与质量标准要求相对关系的不同,正态分布下的过程能力指数计算方法,大致可分为下列四种情况。
1.双侧公差,对称分布,中心重合。
这是产品质量标准要求的公差双侧对称分布,其公差中心M与过程质量特性分布中心μ相重合,无偏移(如图1所示)。其过程能力指数Cp为:
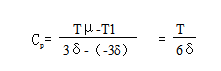
式中:Tμ为产品质量标准要求的规格上限值;
T1为产品质量标准要求规格下限值;
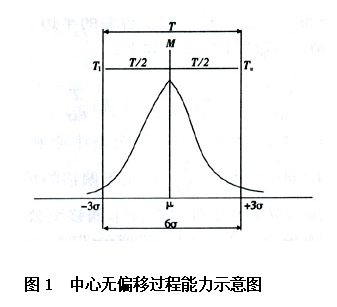
由上式可知,Cp值越大表明过程能力越强。此时,对人员、设备等过程影响因素的控制要求迫近制成酏 越高。当Cp值大低时,则不能保证过程质量满足标准要求,导致出现过多的不合格品。因此,Cp值的选择既要考虑产品质量满足要求,又要考虑过程的经济性。
表面看,当Cp=1时似乎既满足要求,又比较经济,但由于过程的随机波动性难以避免,分布中心的波动和偏移也难以避免,必然使不合格的风险增加。因此,Cp=1并不是最佳选择。在实际工作中,要适当增大Cp值,以确保过程能力满足要求。
2.双侧公差,对称分布,中心偏移。
这种情况的公差中心M与过程分布中心μ不重合,有偏移(如图2所示,图中虚线表示虚拟的无偏移情况下的分布曲线,实线为实际有偏移时的过程分布曲线。)
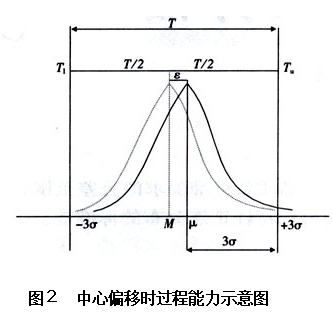
对于这种情况,计算Cp的公式需要进行修正。首先,引入分布中心μ与公差中心M偏移量的概念。设绝对绝对偏移量ε,相对偏移量k :
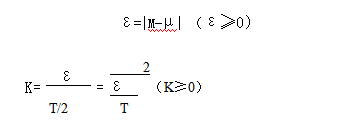
因为µ与M之间的偏移,引起了“吃容差”的现象。当过程分布中心向右偏移时(见图2),会吃上偏差(右半边的偏差);当分布中心向左偏移时,会吃下偏差(左半边的偏差)。这时,过程出现不合格吕的危险首先出现在被吃掉容差的一边。因此,计算过程能力指数时,可以只考虑分布中心偏移后引起喷气发动机容不得差的半边。按照图2的情况,CP的计算公式如下:
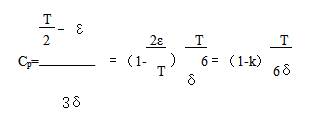
当µ=M ,即分布中心与公关中心相重合时,ε=0、κ=0,导致CP= ,这是无偏移的情况。
当µ与M发生相对偏移,且µ偏移至公差的上限T1或偏至下限 ,即µ=Tu或µ=T1时,ε=T/2、κ=1、CP=0(当偏移使µ越过Tu或T1时,ε>T/2、K>1、CP=0),表明过程能力严重不足,必须停产整顿,分析原因并采取措施纠正分布中心的严重偏移。
3.单向公差,只有上限要求。
有些产品的质量特性(如机械产品的清洁度和形位公差,药品中的杂技含量等),只给出了公差的上限要求并希望越小越好,而没有下限要求。此时,过程能力指数的计算公式如下:
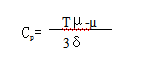
当µ=Tu时,CP=0,表示过程中心偏移至公差上限,过程能力严重不足,产生的不合格品率可能高达50%。
当µ>Tu时,令CP=0,表示过程能力更加不足。
发生上述两种情况都必须停产整顿,对过程进行改进,纠正过程中心的严重偏移情况,以便提高过程能力。
4.单向公差,只有下限要求。
有些产品的质量特性(如机械产品的机械强度,电气产品的耐电压强度、寿命、可靠性),都要求不低于某个下限值,而对上限没有限制且越高越好。在这种情况下,过程能力指数的计算公式如下:
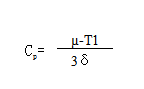
2021/1/14 16:29:57
2021/1/27 17:05:39
2021/3/10 15:48:49
2021/4/8 14:42:32
2021/1/8 16:32:33

我们不单提供专业的软件与服务,我们同时也为客户系统的运行提供理论与经验支持,分享我们在质量管理领域的相关经验与知识!