除非实验者有一个误差的事先估计值，或假设某些交互作用可忽略，否则必须反覆设计以得到一个误差的估计值，

如2³因子实验必须以2个集区来进行且ABC被交络， 实验者决定反覆设计4次，如下图，

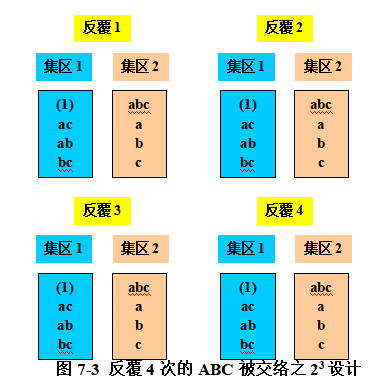
由上图(7-3)与其ANOVA表知，交互作用ABC的信息是完全丧失，因每次反覆中ABC均与集区交络，此称之为完全交络(Completely Confounded)。

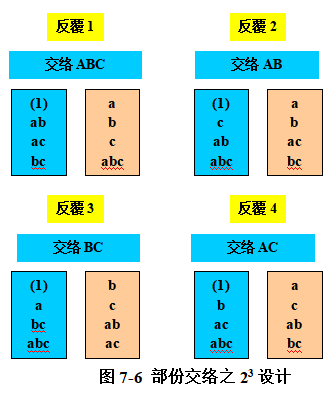
如上图(7-6)，仍是2³因子实验，反覆设计4次，但每次反覆所交络的交互作用却不一样，如，

◎ 反覆1交络ABC、反覆2交络AB、反覆3交络BC、反覆4交络AC，

◎ ABC的信息可由反覆2, 3, 4资料得知、AB的信息可由反覆1, 3, 4资料得知、AC的信息可由反覆1, 2, 4资料得知、AC的信息可由反覆1, 2, 3资料得知。

称此可得到3/4信息的交互作用，因为4次反覆中有3次反覆无被交络，Yates(1937)称比值3/4为交互作用的相对信息(Relative Information for the Confounded Effect)，此设计称之为部分交络(Partial Confounding)。另其ANOVA表如下，

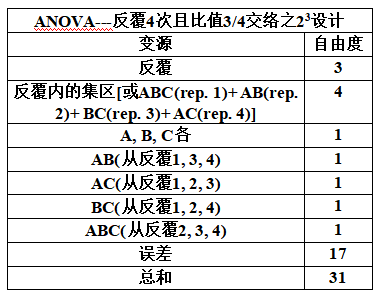
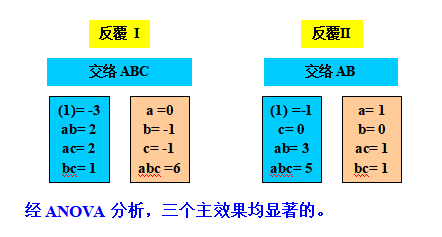
范例 -- 一个部份交络之2³设计

考虑范例 6-1，探讨有关碳酸百分比(A)、操作压力(B)、速度(C)，对碳酸饮料充填高度影响之研究，假设每一批糖浆只能测试4种处理组合，因此，每一次23设计之反覆须在2个集区里进行，计反覆2次，反覆 I 交络ABC、反覆II 交络AB，其资料如下，