判异准则有二类：

(1) 点子出界(包括压线)就判异；

(2) 界内点排列不随机则判异。(原则上有无穷多种)。

模式1  点子屡屡接近管制界限

此模式中，『接近』系指距离管制界限在1s范围内(下图为3点中有2点接近管制界限判异)。

此时属下列情况的，点子排列不随机判异：

(1) 连续3点中，至少有2点接近管制界限；

(2) 连续7点中，至少有3点接近管制界限；

(3) 连续10点中，至少有4点接近管制界限。

模式2  键

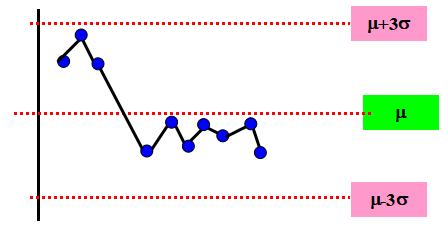
上图表示质量特性值分布的平均值m向出现键的一侧偏移(7点键)。

(1) 在管制图中心线一侧连续出现的点称为键，其中包含的点子数目称为键长。当键长³ 9，则判异。

(2) 分析其a，

P(中心线一侧出现长为9的键)

= 2*(0.9973/2)^9 = 0.0038 = a9

P(中心线一侧出现长为7的键)

= 2*(0.9973/2)^7 = 0.0153 = a7

a7 / a9 = 4

过去采7点键判异。目前多国改采9点键判异。

模式3  间断键

间断键是指键中个别点子跳到中心线的另一侧的键。

(1) 连续11点中，至少有10点在一侧；(下图)

(2) 连续14点中，至少有12点在一侧；

(3) 连续17点中，至少有14点在一侧；

(1) 连续20点中，至少有16点在一侧。

依机率计算，上述四条判异准则的显著性水平分别为：

a1 = 1.14%    a2 =1.25%

a3 =1.22%       a4 =1.12%

由判异准则知，其(四种状况) a 分别均大于0.01，偏大，建议不予使用，除非增加判异准则中的点子数目。

模式4  倾向

下图示中出现有下降倾向(7点下降倾向)，表下品质特性值分布的平均值m 随时间而减少。点子递增或递减的状态称之倾向或趋势。

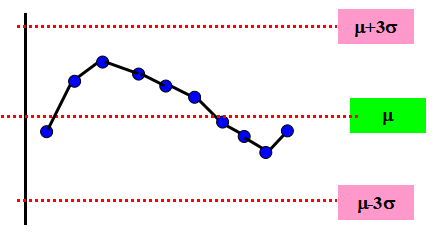
◎ 下降(上升)倾向，后面的点子一定要低(高)于或等于前面的点子，否则倾向中断，须重新起算。

◎ 过去为7点倾向判异，即连续7点上升或下降则判异。目前改为6点倾向判异。

证明：  P(n点倾向) = [2(0.9973)^n] /n!

P(5点倾向) = [2(0.9973)^5] /5!= 0.01644 = a5

P(6点倾向) = [2(0.9973)^6] /6!= 0.00273 = a6

P(7点倾向) = [2(0.9973)^7] /7!= 0.00039 = a7

由于a6 = 0.00273，最接近谢华特的a0= 0.0027，故6点倾向判异是合适的。

模式5  点子集中在中心线附近

◎ 『中心线附近』即指『中心线附近±1s的范围内』。

◎ 下图的现象表示质量特性值分布的标准差s减小。切记此现象亦可能异常，须检查下列二种情况：

(1) 是否应用了假数据，有弄虚作假现象；

(2) 是否分层不够。

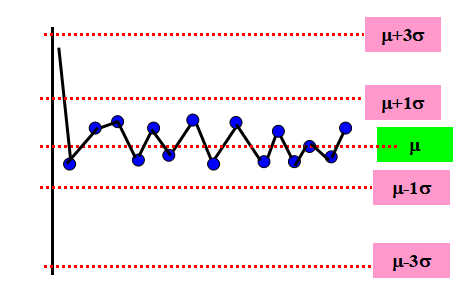
依机率计算：

连续14、15、16个点集中在中心线附近的a为

a14 = 0.68268^14 = 0.00478

a15 = 0.68268^15 = 0.00326

a16 = 0.68268^16 = 0.00223

※ 模式5的 a 取为a15 = 0.00326，比较接近判异准则(1)的a0 = 0.0027。

模式6  点子作周期性变化

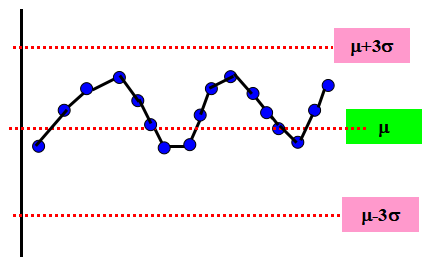
◎ 下图的现象表示点子呈周期性变化。产生其原因有下列二种情况：

(1) 操作人员疲劳；(2) 原材料发送有问题

(3) 热累积或应力累积。

※消除上述周期性变化可使产品质量更加稳定。