2.3 统计在现代社会所扮演的角色

『以事实(数字)作决策』

◎ 政治经济---民调、得票率预测、失业率预测、各项经济指标

◎ 商业方面---市场占有率、利率、汇率

◎ 企管方面---物管、人管、财管、品管

◎ 工程方面---质量、可靠度、交通流量

◎ 农业方面---品种改良、生产量、成功率与存活率

◎ 医药方面---流行病的感染模式、成功率与存活率

◎ 教育方面---教学评鉴、犯罪率

◎ 观光方面---旅游景点的受欢迎程度、周休二的影响

2.4 统计学的发展

◎ 源于1世纪，领导者或君主为了解国家(State)的人口、经济、生产、税赋、天文与气候等。

◎ 直到18世纪左右，主要偏向资料与图形显示的范围，即所谓叙述统计学(Descriptive Statistics)---将资料予以分析后，用数据、模式或图表陈示出来。

◎ 19世纪末和20世纪初，演变包括资料的解释、资料分析归纳、更精确的估计与检定结果、与模式建构等，即所谓推论统计学(Inferential Statistics)或分析统计学(Analytic Statistics)---由随机描样，经样本统计量去推论母体参数，或检定母体参数。对动态资料则有趋势分析、建构模式与预测的功能。

现代统计学大师

1、 Karl Pearson, (1875-1936)---介绍简单的统计量，如众数、标准差及相关系数，尤其回归分析观念和卡方检定都为其贡献。

2、 R. A. Fisher, (1890-1962)---提出小样本统计方法，并建立一致性、有效性、充分性、最大概似法等，提出实验设计，另其对常态分配和t分配的理论与应用都有极大贡献。

3、 J. Neyman, (1894-1981) and Egon Pearson, (1895-)---在估计与检定方面提供理论基础，如提出型I、型II误差及检定力、信赖区间等观念。

4、 A. Wald, (1902-1950)---统计决策理论之始祖。

数学、社会科学与统计学之关系

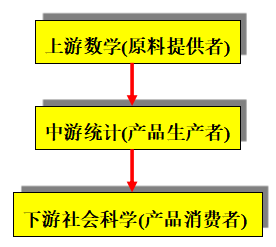
做统计工作时，须注此意数学与统计不同之处

1、 『100/300 = 1/3』，数学式100/300 = 1/3是恒等式，但在统计却有不同的意义。如于一母体中抽3人，其中有1人是男生，则男生所占样本的比例是1/3，如此可能无证据说明此母体中的男女生比例不是各占一半；但倘于此母体中抽300人，其中有100人是男生，则男生所占的样本比例为1/3，如此已有证据说明此母体内男女生比例不是各占一半。

2、 『49/100 ¹ 1/2』，在数学上此式是对的，但在统计检定时，倘于此母体中抽100人，其中有49人是男生，则男生所占的样本比例为49/100，虽然49/100 ¹ 1/2，但可能无足够证据说明此母体内男生比例不是1/2的结论。

统计计算常用软件

『Excel、Minitab、Matlab』、SAS、SPSS、Statistica，QSmart SPC

 2.5 统计资料的整理与描述

研究自然或社会现象，首先要搜集相关的统计资料。接着对所搜集的资料进行处理描述，并制作统计图表，以简洁、有系统的方式，陈示说明资料的主要内容与特性，使之一目了然。

藉由统计资料去了解母体的特性(参数)，常用代表集中趋势的统计量，如样本的平均值；与代表离散的统计量，如样本的变异数或标准差。此即叙述统计量。

(Measures of Central Tendency---Location)

(Measures of Dispersion---Scale)

 2.5.1 统计资料的搜集

一般资料依性质可分为：连续型资料与离散型资料

1. 连续型资料(Continuous Data)：如量测身高、体重、容量、重量、长度等资料，它是一种计量尺度(Metric Sacle)，而且理论上可以量到小数点以下几位的数据。

2. 离散型资料(Discrete Data)：它是一种计数尺度，又细分三型---类别尺度、顺序尺度、比率尺度。

(1) 类别尺度(Nominal Scale)---依资料性质分类并给予特别数值或代号。如女性= 0、男性= 1；合格= ○、不合格= ×；红色= 1、黄色= 2、蓝色= 3。此类别表示之数值或记号只区分类别，没有大小、顺序或比率关系。其仅能计算某类别代号出现的次数或频率，其计算平均数则无意义。

(2) 顺序尺度(Ordinal Scale)--- 依资料的重要性、强弱、好坏程度区分，给予大小不等的数值。如小学= 1、中学= 2、大学= 3、研究所= 4；很便宜= 1、便宜= 2、一般= 3、贵= 4、很贵= 5。此类别虽在等第上有好坏、高低之分别，但无从比较差距。

(3) 比率尺度(Ratio Scale)---以某一特定对象为基准，其他现象相对于此一标准的比值。例如，经济成长率、人口成长率。

2.5.2 资料处理与展示---统计图表

人类辨识影像图形的能力，一般优于辨识数字与文字。千言万言的说明叙述，有时反不及图表的效果。『字不如表，表不如图』。制作统计图表，即以简洁、有系统的方式，陈示说明资料的主要内容与特性，使之一目了然。

常用统计图表

(a) 次数分配或频率表---直方图

(1) 确定所须组数。

(2)计算全部数据的全距(Range)。R = max-min。并求出组距C = 全距/组数

(3) 求出各组的组距与组界

(4) 确定各组的频数    (5) 作直方图

例题：某技术员用车床车制螺丝，要求其直径为10mm。为了了解该技术员的加工质量，抽查其加工的100个螺丝，分别测得其直径数据100个。

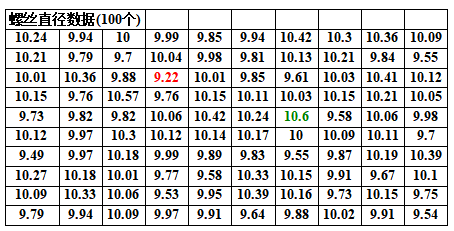
Max. = 10.60； Min. = 9.22；

Range = 1.38；  k = 7 (n =100)；

组距 = 1.38/7 = 0.192 ~ 0.2

为使得所有数据不会落在组界上，并保证最小值9.22落在第一组内，故取第一组的组下限等于最小值减去最小量测单位的一半(即0.01/2 = 0.005)。则

第一组的组下限 = 9.22 – 0.005 = 9.125

第一组的组上限 = 第一组的组下限+组距

= 9.215 + 0.2 = 9.415

接着，确定各组的频数

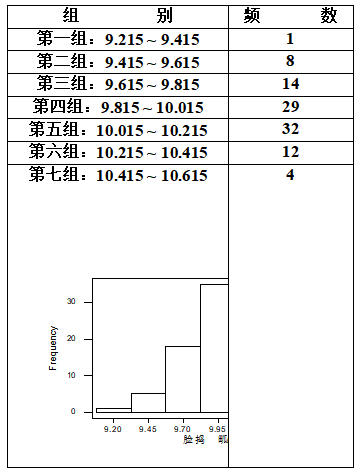
最后作直方图 

◎ 直方图可以种方式表示：

(1) Frequency    à (2) Cumulative Frequency

(3) Percent     à (4) Cumulative Percent

[(3-1) Relative Fequency à (3-2) Cumulative Relative Frequency]

(5) Density      à (6) Cumulative Density

◎ 螺丝直径落在直方图的可能性大小是以其高度表示，另由数学应用方便的角度观之，各直方的面积表示可能大小，由于各组的组距，即直方的宽度是相等的，因此用直方面积表示与用直方的高度表示是相同的。