基本概念

凡质量特性量测值属于连续性的数据，且制程或批之质量假设呈现常态分配且峰态与偏态均为零。或有鉴于检测成本昂贵、破坏性检验与样本数小者，则采计量值抽样计划。并以样本之平均值与标准差，取代计数值之抽样计划。

抽样计划之设计

※规定生产者冒险率(α)之抽样计划

※ 规定消费者冒险率(β)之抽样计划

※规定生产者冒险率(α)与消费者冒险率(β)之抽样计划

规准型抽样计划基本原理

第一种

假设产品的某项主要品特性已知为常态分配，兹抽取n个样本，根据其样本平均值与样本标准差s，分别作为母体平均值μ与标准差σ的估计值，再订定合格判定上、下限可算出所分配之常态分配曲线在合格判定界限外的面积，此即该批产品的估计不合格率p，若 p 最大允收不合格率M，允收该批，反之拒收之。

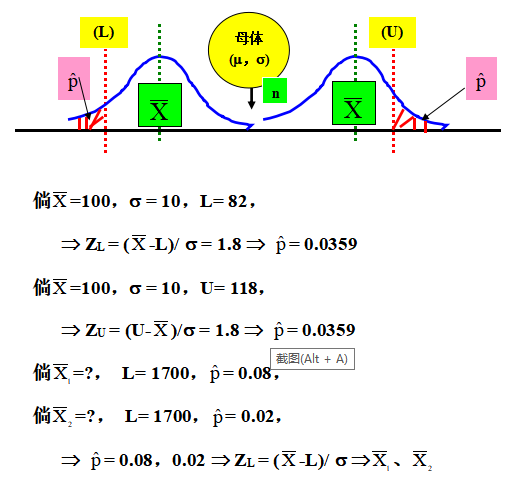
第二种

另一种方式是将最大允收不合格率M，利用某方式转换为一个以单位标准差数(Z值)表示之允收常数k值。于是抽n个样本，算出样本平均值与样本标准差s(分别作为m与s的估计值)，再利用Z_U = (U-X)/3σ  (或Z_L = (X-L)/ 3σ)(如σ已知)之方式将转换为单位标准差数，此时若离上限U(或下限L)愈远则Z_U(或Z_L)愈大，即表不合格率愈低，故在Z_U ≧k(或ZL≧ k)时允收，ZU < k (或Z_L < k)时拒收。Z_U = (U-X)/3σ≧ k的允收基准可改为 X≦ U-ks = A，若样本平均 X≦ A允收送验批，反之拒收。

规准型---JIS Z9003表(单抽)，

◎ 适用于标准差已知之情况，并规定α= 5%、β = 10%。

◎ 假设送验批之质量特性为常态分配，抽样表分为两部份---保证批平均值与保证批不合格率。使用如下：

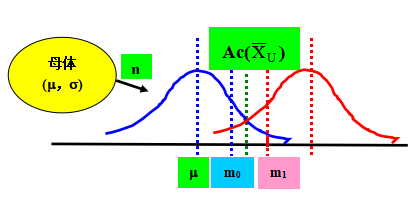
m₀ (希望合格批(生产者冒险率之观点)的平均值)

m₁ (希望不合格批(消费者冒险率之观点)的平均值)

(m₀ -> a = 5% -> K_α= 1.6449)

(m₁ -> b = 10% -> K_β= 1.2816)

(m₁ – m₀ )/( σ/n^0.5 )= (Kα+  K_β) = 2.9265

G₀ = Ka / n^0.5

1、单边规格

(1) 保证批平均值(G₀法)

(A) 双方议定m₀ 、m₁ 。

(B) 决定送验批的标准差σ

(C) 决定抽样计划---利用抽样表决定样本大小n及系数G₀。

a. 约定上限时(希望平均值低)，即m₀ < m₁时，计算(m₁- m₀)/ σ值

b. 约定下限时(希望平均值高)，即m₀ > m₁时，计算(m₀- m₁)/ σ值

c. 利用抽样表由| m_1-m₀|/σ值，得n及G₀