2.6 样本统计量(统计量)(Sample Statistic)

统计图表可方便展示资料，但对于资料的深入分析，其精确度与广度仍不足。为了研究母体的特性(参数)，仍须用一些统计量测数，借以了解母体的特性。常用的统计量测数为代表集中趋势统计量、代表离散统计量与形状统计量，来表达母体的分配情形。这些样本统计量亦称之样本的特征值。

2.6.1集中趋势统计量

集中趋势统计量是用来衡量所有观测值聚集的中心位置---(算术)平均数、中位数、四分位数、众数、截尾平均数

(a) 算术平均数(Arithmetic Mean)

在一般未分组的原始资料中，有n个观测值，其集合为{x1, x2, …, xn |nÎN}，则其算术平均数

=(x1 + x2 + …+ xn)/n = (xi)/n

对于分组资料，假定资料共有n个观测值分为m组，令xi为第i组观测值之组中点，fi为该组观测值相对应的次数，åfi = n。则其算术平均数为

=(x1f1+x2f2+…+xmfm)/n = (xi fi)/n

 (b) 中位数(Median)

中位数又称为二分位数，是一种由小至大顺序数列的中心项。将某笔资料n个观测值由小而大顺序排列，则其中间位数的观测值即为中位数。若n为奇数，则第(n+1)/2位数的观测值为中位数。若n为偶数，中位数即为第n/2位数与第(n/2)+1位数观测值的算术平均数。

(c) 四分位数(Quartile)

将观测值由小至大顺序数列按位数分为四等分，Q1 , Q2 , Q3为其位数等分点之观测值。第0个四分位(Q0)即是最小值，第1个四分位(Q1)是第25%的值，第2个四分位(Q2)是第50%的值(即中位数)，第3个四分位(Q3)是第75%的值，第4个四分位(Q4)即是最大值。

(d) 众数(Mode)

众数是指统计资料中出现之次数最频繁的观测值。

(e) 截尾平均数(Trimmed Mean)---奥运体操评分标准

系考虑算术平均数容易受两端特别远离中心位置观测值的影响，有时不能确切描述观测值集中趋势。即截头去尾的方法，将Q1以下与Q3之上的观测值排除，再计算Q1与Q3之间的观测值的算术平均数。

2.6.2离散趋势统计量

离散趋势统计量是用来测量所有观测值偏离中心的程度---全距、四分位间距、平均绝对偏差、变异数与标准差、变异系数等

(a) 全距(Range)

Range = Max. –Min.

(b) 四分位间距(IQR, Inter-Quartile Range)

四分位间距= Q3-Q1

(c) 平均绝对偏差(MAD, Mean Absolute Deviation)

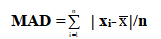
(d) 变异数与标准差(Variance and Standard Deviation)

若有N个母体观测值{x1, x2, …, xN}，且母体平均值为m，则母体变异数为

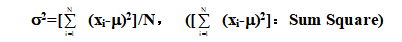
对于样本资料{ x1, x2, …, xn}，则样本变异数为

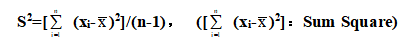
变异数是取观测值与母体平均数差之平方和，所以变异数的单位与原观测值所用的单位不同。为取一致可将变异数的开平方根，则s 称之母体标准差，作为对应之离散量。另样本标准差则相对为S。

对于分组资料，假设资料分为m组共有n个观测值，令xi为第i组观测值之组中点，fi为该组观测值相对应的次数， åfi = n。则样本变异数为

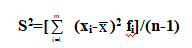
(e) 变异数系数(CV, Coefficient of Variance )

CV =(标准差/平均值)

2.6.3 形状统计量

形状统计量系用量测一组资料对称与否，与分布形状峰度之高低---分别为偏态系数与峰态系数。

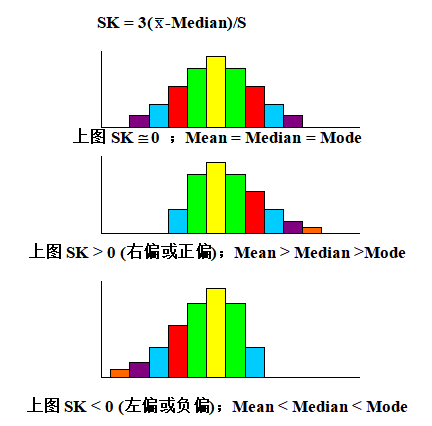
(a) 偏态系数(Skewness)

偏态系数(SK)是对资料分配偏往某一方的趋势(Tendency)。SK的值必介于 –3与3之间。其定义

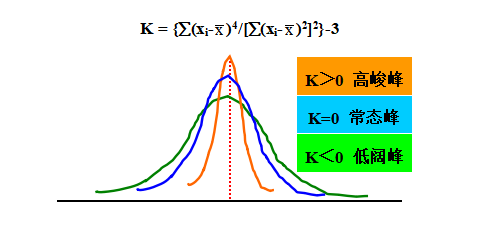
(b) 峰态系数(Kurtosis)

峰态系数(K)是对资料分配峰度(Peakedness)的程度。其定义：